MATEMÁTICA INSTRUMENTAL
Considere a função %7D%7D%7D%3D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7B8%7D%7Bx%7D%2B%7B15%7D "f(x) = x^2 - 8x +15")
, analise as seguintes afirmações:
I. As raízes de f(x) são 3 e – 5 .
II As coordenadas onde o gráfico de f(x) intercepta o eixo y são (0,15).
III. O gráfico será uma parábola com concavidade voltada para cima, pois o “a” é positivo.
IV. A função possui ponto máximo na coordenada (4,-1)
E correto o que se afirma em
II e III apenas
I e II apenas
I e III apenas
I, II e III apenas
I, III e IV apenas
Atenção!!
“Vamos aguardar ordem do homem-bala para proceder à contagem decrescente: cinco, quatro...O homem bala do circo da UBI irá realizar uma grande atração. E ele será arremessado de um canhão.” Preocupados com a sua segurança, a equipe do circo contratou um matemático que descreveu a trajetória do homem, segundo a parábola da função: f (x) = 12x – 3x2.
A altura máxima atingida pelo homem bala será de:
3m
12m.
8m
6m
18m
A enfermeira Giovana para facilitar o seu trabalho, elaborou um gráfico onde indica a quantidade ml de um medicamento que deve ser administrado em seus pacientes em função de seu peso em kg. A expressão matemática que relaciona a quantidade de medicamento (y) em função do seu peso (x) é igual a:
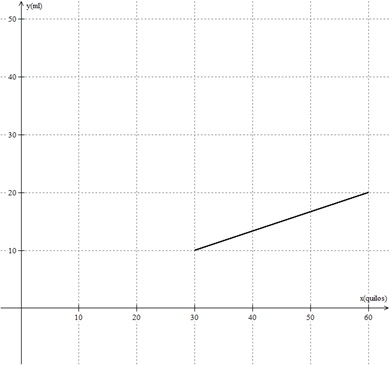
f(x) = x/3
f(x)= -2x
f(x)=x/2
f(x) = 2x/3
f(x) = 2x
A loja de decorações Beba, fez uma organização dos artigos de para promoções de natal. Um vaso e uma cesta de bambu custam juntos R$ 70,00. Dois vasos mais um tapete custam R$ 105,00 e a diferença de preços entre a cesta de bambu e o tapete, nessa ordem, é R$ 5,00.
Com base no exposto analise as afirmativas, a seguir:
I. O valor da cesta é R$ 30,00.
II. A metade do valor da cesta equivale a diferença de preços do vaso e do tapete.
III. O valor do tapete é 2/3 do valor do vaso.
IV. A cesta de bambu tem o menor preço.
É correto o que se afirma em
I e IV apenas
II e III apenas
I e III apenas
I e II apenas
II e IV apenas
Determine os valores de a, b e c para que as matrizes A e B, especificadas, a seguir, sejam iguais.
%7D%7D%5Cright%5D%7D "A=[[1/243,a^2],[64,log_2(1/128)]]")
e 
O valor da soma a + b + c é exatamente:
-8.
-6.
8.
2.
7.
Dadas as matrizes 
e 
então, calculando-se C=(A+B)2, obtém-se a det(c) sendo igual a:
Det(C) = 0.
Det(C) = 176.
Det(C) = 87.
Det(C) = 121.
Det(C) = 181.
Um aplicador deposita R$ 150 000, 00 numa caderneta de poupança. Mensalmente são creditados 0,58% sobre o saldo, estabelecendo a relação %7D%3D%7B150000%7D%7B%7B%5Cleft(%7B1%7D%2C%7B0058%7D%5Cright)%7D%7D%5E%7B%7Bt%7D%7D "S(t)=150000(1,0058)^t")
que expressa o saldo S em função do tempo t em meses.O tempo em meses necessário para que o montante seja igual R$ 158014,15 é aproximadamente:
II e III apenas
I e II apenas
I e III apenas
I, II e III apenas
I, III e IV apenas
Atenção!!
“Vamos aguardar ordem do homem-bala para proceder à contagem decrescente: cinco, quatro...O homem bala do circo da UBI irá realizar uma grande atração. E ele será arremessado de um canhão.” Preocupados com a sua segurança, a equipe do circo contratou um matemático que descreveu a trajetória do homem, segundo a parábola da função: f (x) = 12x – 3x2.
A altura máxima atingida pelo homem bala será de:
3m
12m.
8m
6m
18m
A enfermeira Giovana para facilitar o seu trabalho, elaborou um gráfico onde indica a quantidade ml de um medicamento que deve ser administrado em seus pacientes em função de seu peso em kg. A expressão matemática que relaciona a quantidade de medicamento (y) em função do seu peso (x) é igual a:
f(x) = x/3
f(x)= -2x
f(x)=x/2
f(x) = 2x/3
f(x) = 2x
A loja de decorações Beba, fez uma organização dos artigos de para promoções de natal. Um vaso e uma cesta de bambu custam juntos R$ 70,00. Dois vasos mais um tapete custam R$ 105,00 e a diferença de preços entre a cesta de bambu e o tapete, nessa ordem, é R$ 5,00.
Com base no exposto analise as afirmativas, a seguir:
I. O valor da cesta é R$ 30,00.
II. A metade do valor da cesta equivale a diferença de preços do vaso e do tapete.
III. O valor do tapete é 2/3 do valor do vaso.
IV. A cesta de bambu tem o menor preço.
É correto o que se afirma em
I e IV apenas
II e III apenas
I e III apenas
I e II apenas
II e IV apenas
Determine os valores de a, b e c para que as matrizes A e B, especificadas, a seguir, sejam iguais.
e
O valor da soma a + b + c é exatamente:
-8.
-6.
8.
2.
7.
Dadas as matrizes e então, calculando-se C=(A+B)2, obtém-se a det(c) sendo igual a:
Det(C) = 0.
Det(C) = 176.
Det(C) = 87.
Det(C) = 121.
Det(C) = 181.
Um aplicador deposita R$ 150 000, 00 numa caderneta de poupança. Mensalmente são creditados 0,58% sobre o saldo, estabelecendo a relação que expressa o saldo S em função do tempo t em meses.O tempo em meses necessário para que o montante seja igual R$ 158014,15 é aproximadamente:
3m
12m.
8m
6m
18m
A enfermeira Giovana para facilitar o seu trabalho, elaborou um gráfico onde indica a quantidade ml de um medicamento que deve ser administrado em seus pacientes em função de seu peso em kg. A expressão matemática que relaciona a quantidade de medicamento (y) em função do seu peso (x) é igual a:
f(x) = x/3
f(x)= -2x
f(x)=x/2
f(x) = 2x/3
f(x) = 2x
A loja de decorações Beba, fez uma organização dos artigos de para promoções de natal. Um vaso e uma cesta de bambu custam juntos R$ 70,00. Dois vasos mais um tapete custam R$ 105,00 e a diferença de preços entre a cesta de bambu e o tapete, nessa ordem, é R$ 5,00.
Com base no exposto analise as afirmativas, a seguir:
I. O valor da cesta é R$ 30,00.
II. A metade do valor da cesta equivale a diferença de preços do vaso e do tapete.
III. O valor do tapete é 2/3 do valor do vaso.
IV. A cesta de bambu tem o menor preço.
É correto o que se afirma em
I e IV apenas
II e III apenas
I e III apenas
I e II apenas
II e IV apenas
Determine os valores de a, b e c para que as matrizes A e B, especificadas, a seguir, sejam iguais.
e
O valor da soma a + b + c é exatamente:
-8.
-6.
8.
2.
7.
Dadas as matrizes e então, calculando-se C=(A+B)2, obtém-se a det(c) sendo igual a:
Det(C) = 0.
Det(C) = 176.
Det(C) = 87.
Det(C) = 121.
Det(C) = 181.
Um aplicador deposita R$ 150 000, 00 numa caderneta de poupança. Mensalmente são creditados 0,58% sobre o saldo, estabelecendo a relação que expressa o saldo S em função do tempo t em meses.O tempo em meses necessário para que o montante seja igual R$ 158014,15 é aproximadamente:
f(x) = x/3
f(x)= -2x
f(x)=x/2
f(x) = 2x/3
f(x) = 2x
A loja de decorações Beba, fez uma organização dos artigos de para promoções de natal. Um vaso e uma cesta de bambu custam juntos R$ 70,00. Dois vasos mais um tapete custam R$ 105,00 e a diferença de preços entre a cesta de bambu e o tapete, nessa ordem, é R$ 5,00.
Com base no exposto analise as afirmativas, a seguir:
I. O valor da cesta é R$ 30,00.
II. A metade do valor da cesta equivale a diferença de preços do vaso e do tapete.
III. O valor do tapete é 2/3 do valor do vaso.
IV. A cesta de bambu tem o menor preço.
É correto o que se afirma em
I e IV apenas
II e III apenas
I e III apenas
I e II apenas
II e IV apenas
Determine os valores de a, b e c para que as matrizes A e B, especificadas, a seguir, sejam iguais.
e
O valor da soma a + b + c é exatamente:
-8.
-6.
8.
2.
7.
Dadas as matrizes e então, calculando-se C=(A+B)2, obtém-se a det(c) sendo igual a:
Det(C) = 0.
Det(C) = 176.
Det(C) = 87.
Det(C) = 121.
Det(C) = 181.
Um aplicador deposita R$ 150 000, 00 numa caderneta de poupança. Mensalmente são creditados 0,58% sobre o saldo, estabelecendo a relação que expressa o saldo S em função do tempo t em meses.O tempo em meses necessário para que o montante seja igual R$ 158014,15 é aproximadamente:
I e IV apenas
II e III apenas
I e III apenas
I e II apenas
II e IV apenas
Determine os valores de a, b e c para que as matrizes A e B, especificadas, a seguir, sejam iguais.
e
O valor da soma a + b + c é exatamente:
-8.
-6.
8.
2.
7.
Dadas as matrizes e então, calculando-se C=(A+B)2, obtém-se a det(c) sendo igual a:
Det(C) = 0.
Det(C) = 176.
Det(C) = 87.
Det(C) = 121.
Det(C) = 181.
Um aplicador deposita R$ 150 000, 00 numa caderneta de poupança. Mensalmente são creditados 0,58% sobre o saldo, estabelecendo a relação que expressa o saldo S em função do tempo t em meses.O tempo em meses necessário para que o montante seja igual R$ 158014,15 é aproximadamente:
-8.
-6.
8.
2.
7.
Dadas as matrizes e então, calculando-se C=(A+B)2, obtém-se a det(c) sendo igual a:
Det(C) = 0.
Det(C) = 176.
Det(C) = 87.
Det(C) = 121.
Det(C) = 181.
Um aplicador deposita R$ 150 000, 00 numa caderneta de poupança. Mensalmente são creditados 0,58% sobre o saldo, estabelecendo a relação que expressa o saldo S em função do tempo t em meses.O tempo em meses necessário para que o montante seja igual R$ 158014,15 é aproximadamente:
Det(C) = 0.
Det(C) = 176.
Det(C) = 87.
Det(C) = 121.
Det(C) = 181.